9. 일반적인 구동력에 대한 선형 진동자의 응답
9.1. 구동력을 연속적인 충격 함수로 해석

일반적인 구동력은 위 그림에서 볼 수 있듯이
$$I_k \left( t;\, \dfrac{k}{n},\, \dfrac{1}{n} \right) = \begin{cases} \dfrac{1}{m}F\left( \dfrac{k}{n} \right) & \dfrac{k}{n} \le t < \dfrac{k+1}{n} \\ 0 & \mathrm{else} \end{cases}$$
에 대하여
$$\dfrac{F(t)}{m} = \lim_{n \to \infty} \sum_{k = -\infty}^{\infty} I_k \left( t;\, \dfrac{k}{n},\, \dfrac{1}{n} \right)$$
로 나타낼 수 있습니다. 이를 적분 꼴로 나타내면
$$\dfrac{F(t)}{m} = \int_{-\infty}^{\infty} F(t') \dfrac{\delta(t - t')}{m} dt'$$
이고, 미분방정식
$$\ddot{x} + 2\beta \dot{x} + \omega_0^2 x = \dfrac{\delta(t - t')}{m}$$
의 해를 $G(t, t')$라 하면, 식 (3.8.3)에 의하여
$$G(t, t') = \begin{cases} \dfrac{1}{m\omega_1} e^{-\beta (t - t')} \sin(\omega_1(t - t')) & t \ge t' \\ 0 & t< t' \end{cases}$$
입니다. 따라서
$$\begin{align} x(t) & \displaystyle = \int_{-\infty}^{t} F(t') \dfrac{1}{m\omega_1} e^{-\beta(t-t')} \sin(\omega_1(t-t'))dt' \\[3pt] & = \displaystyle \int_{-\infty}^{t} F(t')G(t, t')dt' \qquad (3.8.4) \end{align}$$
입니다. 여기서 $G(t, t')$을 선형 진동자에 대한 그린 함수라고 부릅니다.
9.2. 일반적인 구동력에 대한 선형 진동자의 응답 예제
Example 3.7. Find $x(t)$ for an exponentially decaying forcing function beginning at $t = 0$ and having the following form for $t > 0$:
$$F(t) = F_0 e^{-\gamma t}$$

① $\dfrac{F_0}{m} = 5$, $\gamma = 0.5$, $\omega_0 = 2$, $\beta = 0.56$

② $\dfrac{F_0}{m} = 5$, $\gamma = 0.5$, $\omega_0 = 2$, $\beta = 2$
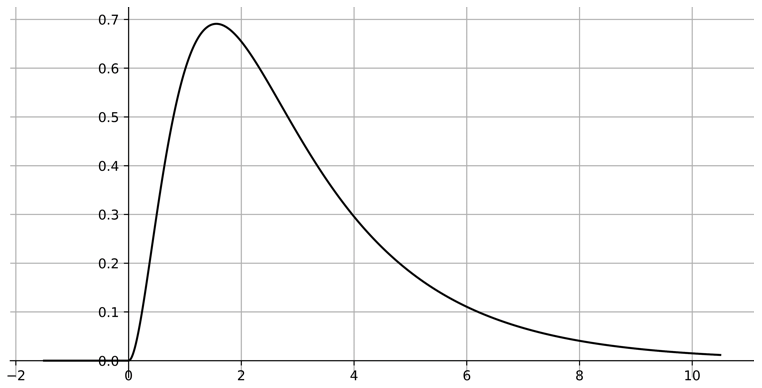
③ $\dfrac{F_0}{m} = 5$, $\gamma = 0.5$, $\omega_0 = 2$, $\beta = 2.5$

'물리 공부 > 역학 1' 카테고리의 다른 글
| [역학 1] 변분법 (2) - 오일러 방정식의 제 2 형태, 종속 변수가 여러 개인 함수 (2) | 2023.02.25 |
|---|---|
| [역학 1] 변분법 (1) - 변분법 문제의 기술, 오일러 방정식 (0) | 2023.02.24 |
| [역학 1] 진동 (8) - 충격형 힘에 대한 선형 진동자의 응답 (0) | 2023.02.23 |
| [역학 1] 진동 (7) - 중첩 원리: 푸리에 급수 (0) | 2023.02.20 |
| [역학 1] 진동 (6) - 물리계: 전기 회로 (0) | 2023.02.20 |
