8. 충격형 힘에 대한 선형 진동자의 응답
8.1. 충격형 힘
충격형 힘이라는 것은 불연속적인 힘을 의미합니다. 믈론 실제 물리적 현상에서 힘이 불연속일 수는 없지만, 진동 시스템의 주기에 비해 매우 잛은 시간에 힘의 급격한 변화가 생길 경우에는 구동력이 불연속 함수일 때와 매우 유사하게 행동할 것입니다. 그리고 충격형 힘이 작용할 때의 선형 진동자의 응답을 통해 구동력이 일반적인 경우에 $x(t)$를 구할 수도 있게 됩니다.
불연속 함수에는 대표적으로 계단 함수(해비사이드 함수), 충격 함수, 디랙 델타 함수가 있습니다. 이 세 가지 경우에 대해서 선형 진동자의 응답을 살펴보겠습니다.
8.2. 계단함수
8.2.1 $\beta < \omega_0$인 경우
계단 함수는 다음과 같이 정의됩니다.
$$H(t;\, t_0) = \begin{cases} 0 & t<t_0 \\ a & t > t_0 \end{cases}$$

이제 $\displaystyle \frac{F(t)}{m} = \begin{cases} 0 & t < t_0 \\ a & t > t_0 \end{cases}$이고, 초기 조건이 $x(t_0) = 0$, $\dot{x}(t_0) = 0$인 경우를 살펴봅시다. $\omega_1 = \sqrt{\omega_0^2 - \beta^2}$에 대하여 $t>t_0$일 때 방정식
$$\ddot{x} + 2\beta \dot{x}+ \omega_0^2x = a$$
의 일반해는
$$x(t) = e^{-\beta(t-t_0)}[A_1 \cos(\omega_1 (t-t_0) ) + A_2\sin(\omega_1 (t-t_0) )] + \dfrac{a}{\omega_0^2}$$
이고, 초기 조건을 대입하면
$$A_1 = -\dfrac{a}{\omega_0^2}, \qquad A_2 = -\dfrac{\beta a}{\omega_1\omega_0^2}$$
이므로
$$x(t) = \dfrac{a}{\omega_0^2}\left[ 1 - e^{-\beta(t-t_0)}\cos(\omega_1(t-t_0)) - \dfrac{\beta e^{-\beta(t-t_0)}}{\omega_1} \sin(\omega_1(t-t_0)) \right]$$
을 얻습니다. 아래 그래프는 $a = 12$, $\omega_0 = 2$, $\beta = 0.56$인 경우를 나타낸 것입니다.

8.2.2. 계단함수: $\beta \ge \omega_0$인 경우
$\beta \ge \omega_0$라면 어떻게 될까요?
먼저 $\beta = \omega_0$일 때는 $\omega_1 \rightarrow 0$의 극한을 취해봅시다. 그러면
$$x(t) = \dfrac{a}{\omega_0^2} \left[ 1 - e^{-\beta(t-t_0)} \left\{ 1 + \beta (t-t_0) \right\} \right]$$
입니다. 이 해는 미분방정식을 만족시키고, 초기 조건도 만족시킴을 계산해보면 확인할 수 있습니다. 아래 그래프는 $a = 12$, $\omega_0 = 2$인 경우를 나타낸 것입니다.

다음으로 $\beta > \omega_0$일 때는 $\omega_1$ 대신에 $\sqrt{\beta^2 - \omega_0^2} i = \beta_1 i$를 대입합니다. 그러면
$$\begin{align} x(t) & = \dfrac{a}{\omega_0^2} \left[1 - e^{-\beta (t-t_0)}\cos (i \beta_1 (t-t_0)) - \dfrac{\beta e^{-\beta(t - t_0)}}{\beta_1 i} \sin (i \beta_1 (t-t_0)) \right] \\[3pt] & = \dfrac{a}{\omega_0^2} \left[ 1 - e^{-\beta (t-t_0)} \cosh(\beta_1 (t-t_0)) - \dfrac{\beta e^{-\beta (t-t_0)}}{\beta_1} \sinh(\beta_1(t - t_0)) \right] \end{align}$$
입니다. 그리고 이 식도 미분방정식을 만족시키고, 초기 조건도 만족시킴을 확인할 수 있습니다. 아래 그래프는 $a = 12$, $\omega_0 = 2$, $\beta = 2.5$인 경우를 나타낸 것입니다.

8.2.3 계단함수: $\beta$와 $\omega_0$의 대소 관계에 무관한 진동의 방정식
결론은, $\beta$와 $\omega_0$의 대소 관계에 상관 없이 진동의 방정식은 모두
$$\dfrac{a}{\omega_0^2}\left[ 1 - e^{-\beta(t-t_0)}\cos(\omega_1(t-t_0)) - \dfrac{\beta e^{-\beta(t-t_0)}}{\omega_1} \sin(\omega_1(t-t_0)) \right] \qquad (3.8.1)$$
로 나타낼 수 있다는 것입니다.
8.3. 충격 함수
충격함수는 다음과 같이 정의됩니다.
$$I(t;\, t_0,\, \tau) = \begin{cases} 0 & t<t_0 \\ a & t_0 < t < t_0 + \tau \\ 0 & t > t_0 + \tau \end{cases}$$

이제 $\displaystyle \frac{F(t)}{m} = \begin{cases} 0 & t < t_0 \\ a & t_0 < t < t_0 + \tau \\ 0 & t > t_0 + \tau \end{cases}$이고, 초기 조건이 $x(t_0) = 0$, $\dot{x}(t_0) = 0$인 경우를 살펴봅시다. 이 해를 구할 때에는 계단함수의 진동을 이용할 수 있습니다. 왜냐하면 충격 함수는 서로 다른 두 게단함수의 차이로 나타낼 수 있기 때문입니다. 즉,
$$H_1(t;\,t_0) = \begin{cases} 0 & t < t_0 \\ a & t > t_0 \end{cases}, \qquad H_2(t;\,t_0 + \tau) = \begin{cases} 0 & t < t_0 + \tau \\ a & t > t_0 + \tau \end{cases}$$
에 대하여
$$\dfrac{F(t)}{m} = H_1(t;\, t_0) - H_2(t;\, t_0 + \tau)$$
입니다. 따라서 충격 함수에 대한 선형 진동자의 응답은 $F(t) = mH_1(t;\, t_0)$일 때의 해에서 $F(t) = mH_2(t;\, t_0 + \tau)$일 때의 해를 뺀 것과 같습니다. 즉, $t > t_1 + \tau$일 때
$$\begin{align} x(t) & = \dfrac{a}{\omega_0^2} \left[ 1 - e^{-\beta(t-t_0)}\cos(\omega_1 (t-t_0)) - \dfrac{\beta e^{-\beta (t-t_0)}}{\omega_1}\sin(\omega_1(t - t_0)) \right] \\[3pt] & \quad - \dfrac{a}{\omega_0^2} \left[ 1 - e^{-\beta(t - t_0 - \tau)} \cos (\omega_1(t - t_0 - \tau)) -\dfrac{\beta e^{-\beta(t-t_0-\tau)}}{\omega_1} \sin(\omega_1(t - t_0 - \tau)) \right] \\[3pt] & = \dfrac{a e^{-\beta(t-t_0)}}{\omega_0^2} \left[ e^{\beta\tau} \left( \cos(\omega_1(t - t_0 - \tau)) +\dfrac{\beta}{\omega_1} \sin(\omega_1(t - t_0 - \tau)) \right) \right. \\[3pt] & \quad \left. - \left( \cos(\omega_1(t-t_0) + \dfrac{\beta}{\omega_1}\sin(\omega_1(t - t_0)) \right) \right] \qquad (3.8.2)\end{align}$$
이 됩니다. 아래 그래프들은 I에서 살펴본그래프에서 $a $, $\omega_0$, $\beta$의 값은 그대로 두고 $\tau = 8$로 둔 것입니다.



8.4. 디랙 델타 함수
디랙 델타 함수는 다음과 같이 정의됩니다. (엄밀히는 함수가 아니지만 편의상 함수라고 부르겠습니다.)
$$\delta (x) = \begin{cases} 0 & (x \neq 0) \\ \infty & (x = 0) \end{cases}, \qquad \int_{-\infty}^{\infty}f(x)\delta(x)dx = f(0)$$
아주 짧은 시간의 강한 충격을 나타낼 때 주로 쓰이는 함수입니다. 디랙 델타 함수에 대한 선형 진동자의 응답은 충격 함수에 대한 응답에서 $a = \dfrac{b}{\tau}$로 대치하고 $\tau \rightarrow 0$로 극한을 취하면 얻을 수 있습니다.
$$\begin{align} x(t) & = \displaystyle \lim_{\tau \to 0} \dfrac{b e^{-\beta(t-t_0)}}{\omega_0^2 \tau} \left[ e^{\beta\tau} \left( \cos(\omega_1(t - t_0 - \tau)) +\dfrac{\beta}{\omega_1} \sin(\omega_1(t - t_0 - \tau)) \right) \right. \\[3pt] & \quad \left. - \left( \cos(\omega_1(t-t_0) + \dfrac{\beta}{\omega_1}\sin(\omega_1(t - t_0)) \right) \right] \\[3pt] & = \dfrac{b e^{-\beta (t-t_0)}}{\omega_0^2} \left. \dfrac{d}{d\tau} \left( e^{\beta \tau} \cos(\omega_1(t - t_0 - \tau)) + \dfrac{\beta e^{\beta\tau}}{\omega_1} \sin(\omega_1(t - t_0 - \tau)) \right) \right|_{\tau = 0} \\[3pt] & = \dfrac{b e^{-\beta(t - t_0)}}{\omega_0^2} \dfrac{\omega_1^2 + \beta^2}{\omega_1} \sin(\omega_1(t - t_0)) \\[3pt] & = \dfrac{b}{\omega_1} e^{-\beta(t - t_0)}\sin(\omega_1(t - t_0)) \qquad (3.8.3) \end{align}$$
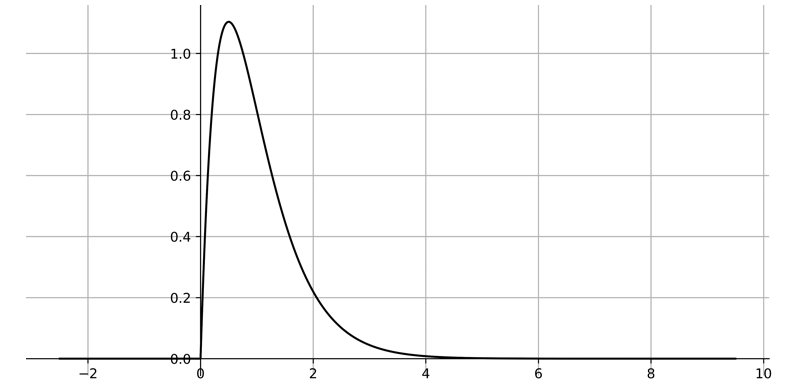
아래 그래프들은 $b = 6$, $\omega_0 = 2$로, $\beta = 0.56, 2, 2.5$로 둔 것입니다.


지금까지 충격형 힘에 대한 선형 진동자의 응답을 살펴봤습니다. 다음 글에서는 임의의 힘에 대해서 선형 진동자의 응답을 살펴보겠습니다.
'물리 공부 > 역학 1' 카테고리의 다른 글
| [역학 1] 변분법 (1) - 변분법 문제의 기술, 오일러 방정식 (0) | 2023.02.24 |
|---|---|
| [역학 1] 진동 (9) - 일반적인 구동력에 대한 선형 진동자의 응답 (0) | 2023.02.24 |
| [역학 1] 진동 (7) - 중첩 원리: 푸리에 급수 (0) | 2023.02.20 |
| [역학 1] 진동 (6) - 물리계: 전기 회로 (0) | 2023.02.20 |
| [역학 1] 진동 (5) - 강제 진동: 사인형 구동력 (0) | 2023.02.20 |
